Introduction: Connecting Your Learning
 People need a common set of rules for performing basic calculations. What does 3 + 5 ⋅ 2 equal? Is it 16 or 13? Your answer depends on the order in which you perform the operations. Mathematicians have developed a standard order of operations that tells you which calculations to make first in an expression with more than one operation. Without a standard procedure for making calculations, two people could get two different answers to the same problem.
People need a common set of rules for performing basic calculations. What does 3 + 5 ⋅ 2 equal? Is it 16 or 13? Your answer depends on the order in which you perform the operations. Mathematicians have developed a standard order of operations that tells you which calculations to make first in an expression with more than one operation. Without a standard procedure for making calculations, two people could get two different answers to the same problem.
The order of operations is defined as the set of rules that tells you the order in which addition, subtraction, multiplication, and division are performed in any calculation.
The order of operations is very important when trying to solve a programming problem or find a GPS location. If the order of operations is done incorrectly, a GPS location could potentially put someone out in the middle of nowhere when he or she was trying to find a store across town, or it could cause a checkbook balancing error in the mobile application that you developed. By paying close attention to the order of operations, a user can successfully navigate to their desired location or calculate the balance for a checking account.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Perform mathematical calculations using the correct order of operations.
Key Terms
Order of Operations
The order of operations is the order that must be followed to simplify math expressions. The universally agreed-upon and accepted order of operations for evaluating a mathematical expression is as follows:
| Please | Parentheses | ( ) | grouping symbols from the inside out |
| Excuse | Exponents | x3 | |
| My | Multiplication | ∙ | as they appear from left to right |
| Dear | Division | ÷ | |
| Aunt | Addition | + | as they appear from left to right |
| Sally | Subtraction | - |
Grouping Symbols
Grouping symbols are used to indicate that a particular collection of numbers and meaningful operations should be grouped together and considered as one number.
Grouping Symbols Commonly used in Mathematics
Parentheses: ( )
Brackets: [ ]
Braces: { }
Fraction Bar: —
- In a computation with more than one operation involved, grouping symbols indicate which operation to perform first. If possible, you should perform operations inside grouping symbols first.
(5 · 5) + 20 = 45 5 times 5 is 25. Adding 20 you get 45.
whereas
5 · (5 + 20) = 125 Here 5 + 20 is performed first as that sum is inside the parentheses. 5 + 20 is 25. Then multiplying 5 and 25, you get 125.
- If there are no parentheses, you should always complete multiplications and divisions first, as they appear left to right, followed by additions and subtractions, as they appear left to right. You can always put your own parentheses into equations using this rule to make things easier for yourself, for example:
| a ÷ b + c · d = (a ÷ b) + (c · d) | 20 ÷ 4 + 5 · 5 = (20 ÷ 4) + (5 · 5) |
Take a look at the following grouping symbols examples.
Example: 9 + (3 · 8)
Since 3 and 8 are within parentheses, they are to be combined first:
= 9 + 24
Then add the terms:
= 33
Thus, 9 + (3 · 8) = 33.
Example: (10 ÷ 0) · 6
Since (10 ÷ 0) is undefined, this operation is meaningless, and no value is attached to it. You write "undefined" as the answer.
Order of Operations in Action
Now that you know about grouping symbols and their importance, you will apply what you learned in the following examples.
Example 1: 21 + 3 ⋅ 12 |
||||
| Step 1: | 21 + 3 ∙ 12 | = | 3 ∙ 12 | Multiplication |
| Step 2: | 21 + 36 | = | 21 + 36 | Addition |
| = | 57 | |||
| Example 2: (15 − 8) + 5(6 + 4) |
||||
| Step 1: | (15 − 8) + 5(6+4) | = | (15 − 8) + 5(6+4) | Simplify inside parentheses first. |
| Step 2: | 7 + 5 ⋅ 10 | = | 7 + 5 ⋅ 10 | Multiply |
| Step 3: | 7 + 50 | = | 7 + 50 | Add |
| = | 57 | |||
| Example 3: 63 − (4 + 6 ⋅ 3) + 76−4 |
||||
| Step 1: | 63 – (4 + 6 ⋅ 3) + 76 – 4 | = | 63 – (4 + 6 ⋅ 3) + 76 – 4 | Simplify inside parentheses (multiplication first then addition) |
| Step 2: | 63 − (4+18) + 76 − 4 | = | 63 − (4+18) + 76 − 4 | |
| Step 3: | 63 – 22 + 76 − 4 | = | 63 – 22 + 76 – 4 | addition and subtraction left to right |
| Step 4: | 41+76 − 4 | = | 41+76−4 | |
| Step 5: | 117 − 4 | = | 117 − 4 | |
| Step 6: | = | 113 | ||
Here is a different way to see the process of using the order of operations to solve a problem.
Example 1: 7 ⋅ 6 − 42 + 15
Evaluate the exponential forms, moving from left to right.
= 7 ⋅ 6 − 16 + 1
Multiply 7 · 6.
= 42 − 16 + 1
Subtract 16 from 42.
= 26 + 1
Add 26 and 1.
= 27
Example 2: 42 + 6 ⋅ (32 + 22)
Evaluate the exponential forms in the parentheses.
= 42 + 6 ⋅ (9 + 4)
Add 9 and 4 in the parentheses.
= 42 + 6 ⋅ (13)
Evaluate the exponential form 42.
= 16 + 6 ⋅ (13)
Multiply 6 and 13.
= 16 + 78
Add 16 and 78.
= 94
Practice Exercises: Order of Operations
Now that you have gained some knowledge, it is time to practice what you have learned. Check your answers after completing the activity to see what you have learned.
Practice Exercise
8 + (32 – 7)
(34 + 18 – 2 · 3) + 11
8(10) + 4(2 + 3) – (20 + 3 · 15 + 40 – 5)
5 · 8 + 42 – 22
4(62 – 33) ÷ (42 – 4)
(8 + 9 · 3) ÷ 7 + 5 · (8 ÷ 4 + 7 + 3 · 5)
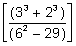 + 5
+ 5
 |
For additional practice with Order of Operations select the following link: Order of Operations Additional Practice Once you complete the additional practice, check to see how well you did by selecting the following link: |
Watch the following Khan Academy video to see additional examples that can help you gain a better understanding of these new concepts.
 |
Math Video Toolkit: |
Summarizing Your Learning
In this lesson, you discovered the importance of the order of operations in mathematics. You learned how one simple problem like 3 + 5 ∙ 2 could lead to two different answers if a standard order is not followed.
Take a few minutes to research how the order of operations relates to various fields. For example, imagine if the banking industry calculated your bank account by subtracting all items that you purchased with your debit card on a particular day before they calculated your paycheck deposit. This would cause a lot of people to overdraw their accounts. The order in which many things are done truly makes a difference to the outcome.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice exercises, it is time for a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
- Complete the Arithmetic Review: Order of Operations.
Resource:
“Exponents, Roots, Factorization of Whole Numbers: Grouping Symbols and the Order of Operations” by Ellis, W., & Burzynski, D. © 2010 retrieved from http://cnx.org/content/m34872/1.2/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This adaption of the lesson, “Order of Operations,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0.