Introduction: Connecting Your Learning
 Do you remember your first cell phone? How about your first GPS (Global Positioning System) or your first game system? Whether you are thinking about the Droid in your pocket or the Nintendo with those clunky plastic cartridges that you had to blow dust out of to get the game to work, you probably had a similar experience with the new technology. You took time to explore every detail of how your new gadget worked. You may know how to "turtle tip" in Mario Brothers or download an app onto your tablet because of all the time spent exploring those items.
Do you remember your first cell phone? How about your first GPS (Global Positioning System) or your first game system? Whether you are thinking about the Droid in your pocket or the Nintendo with those clunky plastic cartridges that you had to blow dust out of to get the game to work, you probably had a similar experience with the new technology. You took time to explore every detail of how your new gadget worked. You may know how to "turtle tip" in Mario Brothers or download an app onto your tablet because of all the time spent exploring those items.
Mathematics is no different. Once you have entered this world, you need to explore and discover the characteristics (properties) that make operations like addition, subtraction, multiplication, and division work. In this lesson, you will examine some of the properties of real numbers.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Identify the basic properties of real numbers.
Presentation
Basic Properties of Real Numbers
The basic properties of real numbers are used to determine the order in which you simplify math expressions. The basic properties of real numbers include the following:
- The Closure Property
- The Commutative Property
- The Associative Property
- The Distributive Property
Take a closer look at each property.
The Closure Properties
Real numbers are closed under addition, subtraction, and multiplication.
That means if a and b are real numbers, then a + b is a unique real number, and a ⋅ b is a unique real number.
For example:
3 and 11 are real numbers.
3 + 11 = 14 and 3 ⋅ 11 = 33  Notice that both 14 and 33 are real numbers.
Notice that both 14 and 33 are real numbers.
Any time you add, subtract, or multiply two real numbers, the result will be a real number.
Although this property seems obvious, some collections are not closed under certain operations.
Here are some examples.
Example 1
Real numbers are not closed under division since, although 5 and 0 are real numbers, 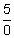 and
and 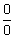 are not real numbers. (You can say that
are not real numbers. (You can say that 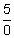 is undefined, which means
is undefined, which means 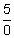 has no meaning. Likewise,
has no meaning. Likewise, 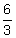 is 2 because you can multiply 3 by 2 to get 6. There is no number you can multiply 0 by to get 5.)
is 2 because you can multiply 3 by 2 to get 6. There is no number you can multiply 0 by to get 5.)
Example 2
Natural numbers are not closed under subtraction. Although 8 is a natural number, 8 − 8 is not. (8 − 8 = 0, and 0 is not a natural number.)
Watch the following video for an additional explanation and examples of the Closure Property.
 |
Math Video Toolkit |
The Commutative Properties
The commutative properties tell you that two numbers can be added or multiplied in any order without affecting the result.
Let a and b represent real numbers.
Commutative Property of Addition |
Commutative Property of Multiplication |
a + b = b + a |
a ⋅ b = b ⋅ a |
Commutative Properties: Examples |
|
3 + 4 = 4 + 3 |
Both equal 7 |
5 + 7 = 7 + 5 |
Both represent the same sum |
4 ⋅ 8 = 8 ⋅ 4 |
Both equal 32 |
y7 = 7y |
Both represent the same product |
5 (3+1) = (3+1) 5 |
Both represent the same product |
(9 + 4) (5 + 2) = (5 + 2) (9 + 4) |
Both represent the same product |
Watch the following videos for a detailed explanation of the Commutative Properties.
 |
Math Video Toolkit |
Practice Exercise: Commutative Properties
It is time to practice what you have learned. You will need a piece of a paper and a pencil to complete the following activity. Write down the proper number or letter that goes in the parentheses to make the statement true. Use the commutative properties. When you are done, make sure to check your answers to see how well you did.
Practice Exercise
6 + 5 = ( ) + 6
m + 12 = 12 + ( )
9 ⋅ 7 = ( ) ⋅ 9
6a = a ( )
4 (k − 5) = ( ) 4
(9a −1)( ) = (2b + 7)(9a − 1)
Example
Simplify (rearrange into a simpler form): 5y6b8ac4
According to the commutative property of multiplication, you can reorder the variables and numbers to and get all the numbers together and all the letters together.
| 5⋅6⋅8⋅4⋅y⋅b⋅a⋅c | Multiply the numbers |
| 960ybac | |
| 960abcy | By convention, when possible, write all letters in alphabetical order |
Use the example above to complete the following practice exercise.
The Associative Properties
The associative properties tell you that you may group together the quantities in any way without affecting the result.
(Let a, b, and c represent real numbers.)
Associative Property of Addition |
Associative Property of Multiplication |
(a + b) + c = a + (b + c) |
(ab) c = a (bc) |
The following examples show how the Associative Properties of addition and multiplication can be used.
Associative Property of Addition |
|||
| (2 + 6) + 1 | = | 2 + (6 + 1) | |
| 8 + 1 | = | 2 + 7 | |
| 9 | = | 9 | both equal 9 |
| Associative Property of Multiplication |
|||
| (2 ⋅ 3) ⋅ 5 | = | 2 ⋅ (3 ⋅ 5) | |
| 6 ⋅ 5 | = | 2 ⋅ 15 | |
| 30 | = | 30 | both equal 30 |
Watch the following videos for a detailed explanation of the Associative Properties.
 |
Math Video Toolkit: |
Practice Exercise: Associative Properties
It is time to practice what you have learned about the Associative Properties. You will need to get out of a piece of a paper and a pencil to complete the following activity. Write down the proper number or letter that goes in the parentheses to make the statement true. Use the Associative Properties. When you are done make sure to check your answers to see how well you did.
The Distributive Properties
When you were first introduced to multiplication, you most likely recognized that it was developed as a description for repeated addition.
Consider this: 4 + 4 + 4 = 3 ⋅ 4
Notice that there are three 4s; that is, 4 appears three times. Hence, 3 times 4. Algebra is generalized arithmetic, and you can now make an important generalization.
When the number a is added repeatedly, meaning n times, we have a + a + a + ⋯ + a (a appears n times)
Then, using multiplication as a description for repeated addition, you can replace a + a + a + ⋯ + a with n (a).
Example 1: x + x + x + x can be written as 4x since x is repeatedly added 4 times.
x + x + x + x = 4x
Example 2: r + r can be written as 2r since r is repeatedly added 2 times.
r + r = 2r
The distributive property involves both multiplication and addition. Take a look at the explanation below.
Rewrite 4(a + b).
STEP 1: You proceed by reading 4(a + b) as multiplication: 4 times the quantity (a + b).
- This directs you to write:
4(a + b) = (a + b) + (a + b) + (a + b) + (a + b) = a + b +a + b + a + b + a + b
STEP 2: Now you use the commutative property of addition to collect all the a′s together and all the b′s together.
- This directs you to write:
4(a + b) = a + a + a + a + b + b + b + b
4a′s + 4b′s
STEP 3: Now, you use multiplication as a description for repeated addition.
- This directs us to write:
4(a + b) = 4a + 4b
- You have distributed the 4 over the sum to both a and b.
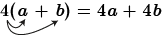
The Distributive Property
The Distributive Property |
|
a (b + c) = a ⋅ b + a ⋅ c |
(b + c) a = b ⋅ a + c ⋅ a |
Because of the commutative property and the convention of writing the variables in alphabetical order, you can also write the following:
b ⋅ a + c ⋅ a as a ⋅ b + a ⋅ c, so (b + c )a = a ⋅ b + a ⋅ c too.
The distributive property is useful when you cannot or do not wish to perform operations inside parentheses.
Examples
Use the distributive property to rewrite each of the following quantities.
2( 5 + 7) = 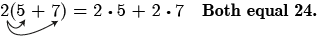
6 ( x + 3) = 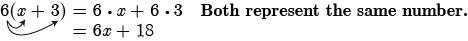
(z + 5) y = 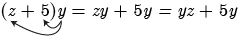
Watch the following videos for a detailed explanation of the Distributive Property.
 |
Math Video Toolkit: |
Practice Exercise: Distributive Properties
Use the distributive property to rewrite each of the following quantities without the parentheses. When you perform operations using the distributive property, it is often called expanding the expression.
The Identity Properties
Additive Identity
The number 0 is called the additive identity since when it is added to any real number, it preserves the identity of that number. Zero is the only additive identity.
For example: 6 + 0 = 6
Multiplicative Identity
The number 1 is called the multiplicative identity since when 1 is multiplied by any real number, it preserves the identity of that number. One is the only multiplicative identity.
For example: 6 ⋅ 1 = 6.
The identity properties are summarized as follows.
| Additive Identity Property |
Multiplicative Identity Property |
If a is a real number, then a + 0 = a and 0 + a = a |
If a is a real number, then a ⋅ 1 = a and 1 ⋅ a = a |
Watch the following Khan Academy videos for an additional explanation and examples of the Identity Property.
 |
Math Video Toolkit: |
The Inverse Properties
Additive Inverses
When two numbers are added together and the result is the additive identity, 0, the numbers are called additive inverses of each other.
Example
When 3 is added to −3, the result is 0: that is 3 + (−3) = 0.
The numbers 3 and −3 are additive inverses of each other.
What is the additive inverse of −15?
Answer: 15
For a more in-depth explanation of additive inverses, watch the following video by Khan Academy.
 |
Multiplicative Inverses
When two numbers are multiplied together and the result is the multiplicative identity, 1, the numbers are called multiplicative inverses of each other.
Example
When 6 and 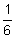 are multiplied together, the result is 1: that is, 6 ⋅
are multiplied together, the result is 1: that is, 6 ⋅ 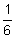 = 1.
= 1.
The numbers 6 and 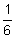 are multiplicative inverses of each other.
are multiplicative inverses of each other.
What is the multiplicative inverse of 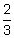 ?
?
Answer: 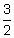
The inverse properties are as follows.
The Inverse Properties
If a is any real number, then there is a unique real number −a, such that a + (−a ) = 0 and −a + a = 0 |
|
If a is any nonzero real number, then there is a unique real number |
|
For a more in-depth explanation of multiplicative inverses watch the following video by Khan Academy.
 |
Exercise: Additive and Multiplicative Inverses
 |
Complete the following exercise to practice what you have learned about the Additive and Multiplicative Inverses by selecting the link below. Additive and Multiplicative Inverses Practice Once you have completed the practice, you can select the following link to see how you did. |
Summarizing Your Learning
Did you know there were so many kinds of properties for real numbers? You should now be familiar with closure, commutative, associative, distributive, identity, and inverse properties. Literal explanations were included to make the symbolic explanations easier to interpret. Take a look at the following Web site for additional explanations of the properties of real numbers.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the exercise questions, it is time for a knowledge check. Note that this is a graded part of this module so be sure you have prepared yourself before starting. |
- Complete the Arithmetic Review: Properties of Real Numbers.
Resource:
“Basic Properties of Real Numbers: Properties of the Real Numbers” by Ellis, W., & Burzynski, D. © 2009 retrieved from http://cnx.org/content/m21894/1.4/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This adaption of the lesson, “Properties of Real Numbers,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0.
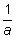 such that a ⋅
such that a ⋅