Introduction: Connecting Your Learning
Mathematics is commonly referred to as the universal language. With the overwhelming popularity of social media, this is becoming increasingly clear. You cannot communicate with others from various walks of life without the common language of mathematics driving your Internet connection, moving satellites, or translating words.
Furthermore, people cannot map the earth from smartphones without computer programmers to generate mathematical algorithms to provide this technology. If you choose to pursue a career in information technology, whether it is in security, networking, mobile applications, or geospatial technology, you will need a certain level of mathematical knowledge.
In this lesson, you will learn how real numbers are ordered, how many categories of numbers exist, and mathematical symbolism that allows you to quickly compare or categorize numbers.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Distinguish between variables and constants.
- Classify numbers into their appropriate sets/subsets.
- Order real numbers.
Presentation
Variables and Constants
A basic distinction between algebra and arithmetic is the use of symbols. In algebra, symbols (usually letters) are used to represent numbers. To solve math problems, you should know what variables and constants are. Here is an introduction to the terms variables and constants.
A variable is a letter or symbol used as a placeholder for an unknown value.
 |
A constant can be a letter or a symbol that represents a fixed number.
|
Look at two examples of situations in which letters are substituted for numbers.
Example 1
Suppose that a student is taking three technology-related classes.
- Each specific class can have one exam per week at most.
- Therefore, in any one-week period, the student may have 0, 1, 2, or 3 exams for the three classes.
- In algebra, the letter X can represent the number of exams the student may have in a one-week period.
- The letter X is a variable since it can represent any of the numbers: 0, 1, 2, 3.
Example 2
Suppose you must report the total number of software programs used in the computer lab during the spring semester at your college.
- Since you do not know this number off the top of your head, you decide to represent it (at least temporarily) with the letter S.
- Later, you make a list of the available software programs and add up the total number. You find there are a total of seven computer software programs being used.
- The letter S, which represents this number then, is 7.
- Since S cannot represent any other values, the value S is constant.
Watch the following videos about variables and constants. You will see additional examples that can help you gain a better understanding of these new concepts.
|
Math Video Toolkit |
Real Numbers
Before learning about real numbers and the aspects that make up real numbers, you will first learn about the real number line.
The study of mathematics requires the use of several collections of numbers. The real number line allows you to visually display (graph) the numbers you are interested in.
A line is composed of infinitely many points. To each point you can associate a unique number, and with each number, you can associate a particular point.
The following words are used to describe points on a real number line.
Coordinate
The number associated with a point on the number line is called the coordinate of the point.
Graph
The point on a number line that is associated with a particular number is called the graph of that number.
How Do I Construct a Real Number Line?
Here are three steps to follow to create a real number line.
- Draw a horizontal line.
- Mark the origin.
Choose any point on the line and label it 0. This point is called the origin.
- Choose a convenient length. Starting at 0, mark this length off in both directions, being careful to make the lengths about the same size.
Now that you have created a number line, it is time see how points on a number line are defined.
Real Numbers
A real number is any number that is the coordinate of a point on the real number line.
Positive Numbers, Negative Numbers
Real numbers whose graphs are to the right of 0 are called positive real numbers, or more simply, positive numbers. Real numbers whose graphs appear to the left of 0 are called negative real numbers, or negative numbers.
The number 0 is neither positive nor negative.
|
Watch the video for a simple explanation of positive and negative numbers on a real number line. |
Subsets of Real Numbers
The set of real numbers has many subsets. Below is a diagram of real numbers. You will see the terms natural, whole, integers, rational, and irrational numbers which are sets of real numbers.
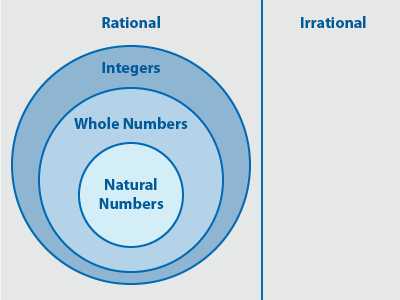
Natural Numbers, Counting Numbers
The letter (N) is the symbol used to represent natural numbers. Natural numbers are also known as counting numbers, and they begin with the number 1 and continue to infinity (never ending), which is represented by three dots (...).
The natural or counting numbers (N): 1, 2, 3, 4 . . . "and so on."
Whole Numbers
The letter (W) is the symbol used to represent whole numbers. Whole numbers are counting numbers from 0 to infinity.
The whole numbers (W): 0, 1, 2, 3, 4 . . .
Notice that every natural number is a whole number.
Integers
The letter (Z) is the symbol used to represent integers. An integer can be 0, a positive number to infinity, or a negative number to negative infinity.
The integers (Z): . . . -3, -2, -1, 0, 1, 2, 3 . . .
Notice that every whole number is an integer.
|
Watch the following video to gain a better understanding of integers. |
Rational Numbers (Fractions)
The letter (Q) is the symbol that is used to represent rational numbers. Rational numbers are sometimes called fractions. They are numbers that can be written as the quotient of two integers. They have decimal representations that either terminate or do not terminate but contain a repeating block of digits. Some examples are below:
−
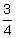= − 0.75 Terminating
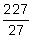= 8.407407407 . . . Non-terminating, but repeating
Some rational numbers are graphed below.
Notice that every integer is a rational number.
You will notice a great many points on the number line that are not discussed. These numbers make up the irrational numbers. They will be examined in detail in an algebra course. An example of an irrational number is π (pi), whose decimal representation does not terminate nor contain a repeating block of digits. An approximation for π is 3.14.
Example: Real Numbers
- Is every whole number a natural number?
- Is there an integer that is not a natural number?
- Is there an integer that is a whole number?
No. The number 0 is a whole number, but it is not a natural number.
Yes. Some examples are 0, −1, −2, −3, and −4.
Yes. In fact, every whole number is an integer.
Now it is your turn to practice. Try answering the following questions on your own and then select Check Answers to see how well you did.
Practice
- Is every natural number a whole number?
- Is every whole number an integer?
- Is every integer a real number?
- Is there an integer that is a whole number?
- Is there an integer that is not a natural number?
|
Watch the following video for a basic overview of the subsets of real numbers with examples to help you apply your new knowledge. |
 |
Complete the following interactive activity to test your knowledge. |
Ordering Real Numbers
Equality Symbols
You know what the equal symbol means and looks like.
If a = b, then a and b are equal, (8 = 8).
To learn about ordering real numbers, think about it this way.
If a real number b is greater than a real number a, their relationship would look like this:
b > a, and b is to the right of a on the number line
Here is an example:
5 > 2 
since 5 is to the right of 2 on the number line
−2 > −5 since −2 is to the right of −5 on the number line.
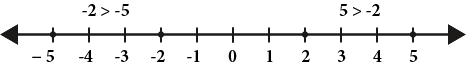
Inequality Symbols
It is important to learn what each inequality symbol means because they are used to order numbers. Take a look at the chart below.
Inequality Symbols |
What does the symbol mean? |
Example 1 |
Example 2 |
Example 3 |
> |
is greater than |
a > b |
a is greater than b |
(8 > 5) |
< |
is less than |
a < b |
a is less than b |
(5 < 8) |
≠ |
is not equal to |
a ≠ b |
a is not equal to b |
(8 ≠ 5) |
≥ |
is greater than or equal to |
a ≥ b |
a is greater than or equal to b |
(a ≥ 8) |
≤ |
is less than or equal to |
a ≤ b |
a is less than or equal to b |
(a ≤ 8) |
If a and b represent two numbers, then a and b are related in exactly one of three ways: either a = b, a < b, or a > b.
Example 1
What integers can replace x so that the following statement is true?
−3 ≤ x < 2
Answer: The integers are −3, −2, −1, 0, 1.
Example 2
Draw a number line that extends from −3 to 5. Place points at all whole numbers between and including −1 and 3.
Answer:
−1 is not a whole number.
Now that you have gained some knowledge, it is time to practice what you have learned.
Practice
Draw a number line that extends from −4 to 4.
Place points at all whole numbers between and including −1 and 4.
Practice
Draw a number line that extends from −4 to 3.
Place points at all whole numbers between and including −2 and 2.
Practice
What integers can replace x so that the following statement is true?
−5 ≤ x <2
 |
It is time to practice on your own. Select the link below to work on practice problems and then select the link to the solutions to see how well you did. Variables, Constants, Real Number Practice Problems Solutions: Variables, Constants, Real Numbers Practice Problems |
|
Watch the following videos to see additional examples that can help you gain a better understanding of these new concepts. |
Summarizing Your Learning
In this lesson, you have been introduced to basic components of a valuable link between societies called mathematics. You have seen the difference between variables (ever-changing components in math) and constants. You have also seen that numbers are categorized, and more importantly, you have seen that some numbers fall into multiple categories. At the conclusion of this lesson you were introduced to the inequality symbol (<, ≤, >, ≥).
As you progress through mathematics you will see how important these symbols are to the world of information technology, specifically to processes that require algorithms, a step-by-step procedure, or linear programming.
Lastly, as you become acquainted with new symbols or terms, you are encouraged to take time to research how each particular concept relates to the field of study you have chosen.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice problems, it is time for a knowledge check. Please note that this is a graded part of this module so be sure you have prepared yourself before starting. |
- Complete the Arithmetic Review: Variables, Constants, and Real Num
Resource:
“Signed Numbers: Variables, Constants, and Real Numbers” by Ellis, W., & Burzynski, D. © 2010 retrieved from http://cnx.org/content/m35027/1.2/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This adaption of the lesson, “Variables, Constants and Real Numbers,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0.