Introduction: Connecting Your Learning
 The purpose of this lesson is to teach you about three common formats for numbers: fractions, decimals, and percents. Percents are often used to interconnect comparative amounts. You have probably seen and used these most often in real-world settings. For example, when you shop, you see various percentage discounts in the stores. Also, when you figure out your taxes or shop around for the best interest rate on a car loan, you use percentages.
The purpose of this lesson is to teach you about three common formats for numbers: fractions, decimals, and percents. Percents are often used to interconnect comparative amounts. You have probably seen and used these most often in real-world settings. For example, when you shop, you see various percentage discounts in the stores. Also, when you figure out your taxes or shop around for the best interest rate on a car loan, you use percentages.
Within the IT field, percentages are used to study how resources are being used on a computer or how much bandwidth is being consumed on a network based upon the maximum capacity of the network. You will also need to be mindful of ratios and proportions used for the screen resolutions of mobile devices in order to properly design a mobile application. In this section, you will learn to convert between each of these formats (decimals, percents, and fractions).
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Describe the characteristics and usefulness of percent notation.
- Convert between fractions, decimals, and percents.
Key Terms
Presentation
Ratios and Percents
A ratio is defined as the comparison of one size of a number to the size of another number. A most convenient number to use when comparing numbers is 100. Ratios in which one number is compared to 100 are called percents.
The word percent comes from the Latin word per centum. The word per means "for each" or "for every," and the word centum means "hundred." Thus, you have the following definition.
Percent means "for each hundred," or "for every hundred."
- The symbol % is used to represent the word percent.
In order to better understand percents, take a look at the following examples.
Notice that 50 of the 100 squares in the grid below have been shaded green. This represents 50% (50 per 100).

50 out of 100 or 50 percent or 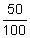 or 50%
or 50%
| Example | |
Problem |
What percent of the grid is shaded?
|
The grid is divided into 100 smaller squares, with 10 squares in each row. 16 squares out of 100 squares are shaded. |
|
The Relationship between Fractions, Decimals, and Percents – Making Conversions
Since a percent is a ratio a ratio can be written as a fraction, and a fraction can be written as a decimal. This means any of these forms can be converted to any of the others. Look at the chart below for detailed information on how to make conversions between fractions, decimals, and percents.
Table 1: Conversion Techniques – Fractions, Decimals, Percents
To Convert a Fraction |
To Convert a Decimal |
To Convert a Percent |
To a decimal: Divide the numerator by the denominator. |
To a fraction: Read the decimal and reduce the resulting fraction. |
To a decimal: Move the decimal point 2 places to the left and drop the % symbol. |
To a percent: Convert the fraction first to a decimal, then move the decimal point 2 places to the right and add the % symbol. |
To a percent: Move the decimal point 2 places to the right and add the % symbol. |
To a fraction: Drop the % sign and write the number "over" 100. Reduce, if possible. |
Review the examples below which provide detailed steps for converting to fractions, decimals and percents.
| Example | ||
Problem |
Convert 12% to a simplified fraction and to a decimal. |
|
| Convert to fraction. | 12% = 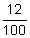 |
Drop the % sign and write the number "over" 100. Reduce, if possible. |
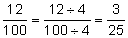 |
Reduce the fraction by dividing the numerator and denominator by the common factor 4. | |
| Convert to decimal. | 12% = 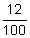 = 0.12 = 0.12 |
You can also just move the decimal point in the whole number 12 two places to the left to get 0.12. |
| Example | ||
Problem |
Convert 0.75 to a percent and to a simplified fraction. |
|
| Convert to percent. | 0.75 = 75% | Move the decimal point 2 places to the right and affix the % symbol. |
| Convert to fraction. | 0.75 = 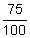 |
To write 0.75 as a fraction, you read the decimal, 75 hundredths, and in fraction form. |
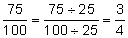 |
Reduce the fraction by dividing the numerator and denominator by 25, a common factor. | |
| Example | ||
Problem |
Convert |
|
| Convert to decimal. | 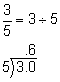 |
Divide the numerator by the denominator. 3 ÷ 5 = 0.6. |
| Convert to percent. | 0.6 = 60% | To write the decimal as a percent, move the decimal point 2 places to the right and affix the % symbol. |
| Example | ||
Problem |
Convert |
|
| Convert to decimal. | 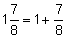 |
Write the mixed fraction as 1 plus the fractional part. |
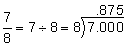 |
Write the fractional part as a decimal by dividing the numerator by the denominator. 7 ÷ 8 = 0.875. | |
| 1 + 0.875 = 1.875 | Add 1 and the decimal number. | |
| Convert to percent. | 1.875 = 187.5% |
Move the decimal point 2 places to the right and add the % symbol. |
| Example | ||
Problem |
Convert 275% to a decimal and to a simplified fraction. |
|
| Convert to decimal. | 275% = 2.75 | Move the decimal point 2 places to the left and drop the % symbol. |
| Convert to fraction (mixed number) |
2.75 = 2 + 0.75 | Write the decimal as a sum of the whole number and the fractional part. |
0.75 = 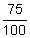 |
Write the decimal part as a fraction. | |
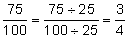 |
Reduce the fraction by dividing the numerator and denominator by a common factor of 25. | |
2 + 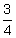 = = 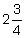 |
Add the whole number part to the fraction. | |
Watch the following Khan Academy video about decimals, percents, and fractions. You will see additional examples that can help you better understand these new concepts.
 |
Math Video Toolkit |
Practice: Converting between Fractions, Decimals, and Percents
 |
Now you get a chance to work some problems. You may use a calculator if you would like. Study each of these problems carefully; you will see similar problems on the lesson knowledge check. Select the following link to complete the practice activity. You will need to get out a piece of paper and a pencil to complete the practice problems. Converting between Fractions, Decimals, and Percents Once you complete the practice activity, check to see how well you did by selecting the following link: Solutions: Converting between Fractions, Decimals, and Percents |
Summarizing Your Learning
Percents are a common way to represent decimal or fractional amounts. Any number that can be written as a decimal, fraction, or percent can also be written using the other two representations. Now that you have finished Lesson 1 in this module, you are encouraged to conduct additional research into how these topics pertain to your particular area of study within the IT world. You probably don't have to look much farther than your computer screen. Most computers have the ability to zoom in or out. This zoom feature is typically characterized with a percentage. With this simple computer feature, you can zoom out to see the whole world on Google Earth or zoom in to see your personal vehicle sitting in your drive way.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice exercises, it is time for a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
- Complete the Percents: Converting between Fractions, Decimals, and Percentages.
Resource:
“Ratios and Rates: Percent” by Ellis, W., & Burzynski, D. © 2010 retrieved from http://cnx.org/content/m34983/1.2/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This is an adaption of the lesson titled,“Converting: Fractions, Decimals, and Percents,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0.

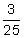 = 0.12
= 0.12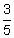 to a decimal and to a percent.
to a decimal and to a percent.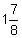 to a decimal and to a percent.
to a decimal and to a percent.