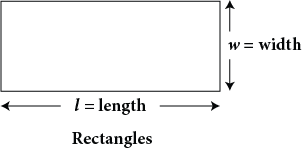WRKDEV100-20011 - Geometric Figures and Solving for Area

Geometric Figures and Solving for Area

Introduction: Connecting Your Learning

student using an iPad for geospatial location mapping Most students in high school and college math ask the question, "When will I ever use this concept in real life?" In reality, geometry has many practical applications to the everyday world as well as the computer world.

Geometry can be interesting when you think about how it is connected to the design of computer applications including real and virtual objects, or if you are trying to determine information about and properties of a geospatial location or area. In this module, you will discuss area of geometric figures and objects. By the end of the module, you should know the meaning and notation for area and the area formulas for some common geometric figures, and be able to calculate the area of some common geometric figures.

Focusing Your Learning

Lesson Objectives

By the end of this lesson, you should be able to:

Calculate the area of common geometric figures.

Presentation

Area

The area of a surface is the amount of square length units contained in the surface.

You will begin by learning the formulas for calculating the area of various geometric figures. Each figure has a certain formula that you need to calculate the area, which is the amount of square length units contained in the surface.

For example, 3 sq. in. means that 3 squares, 1 inch on each side, can be placed precisely on a surface. (The squares may have to be cut and rearranged so they match the shape of the surface.)

Select the following link to see a representation of area using a sheet of paper. You will be able to see how area is measured by dividing the paper into small square units.

Area

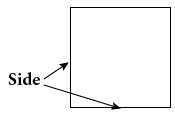
Now that you have a better idea of what area is, look at a square. It has four equal sides and four equal angles: Each angle is 90°. To determine the area of a square, use the following formula.

Area of Square

Area = side ⋅ side = side²

A square with an arrow pointing to the left side and an arrow pointing to the top side

Example

Calculate the area of a square with a side measuring 6 inches. A square with one side length labeled 6 inches

Area = side ⋅ side = side²

Area = 6 in. ⋅ 6 in. = 36 sq. in.

Since the side is 6 in. you would need to multiply 6 times 6 which also means 6².

6 ⋅ 6 or 6²= 36 sq. in.

Example

Calculate the area of a square with a side measuring 9 cm. A square with one side length labeled 9 centimeters

Area = side ⋅ side = side²

Area = 9 cm ⋅ 9 cm = 81 sq. cm

Since the side is 9 cm you would need to multiply 9 times 9 which also means 9².

9 ⋅ 9 or 9²= 81 sq. cm

Now, you will examine area formulas so that you can become familiar with how to find the area of the following geometric figures.

Area Formulas

The area of these geometric figures can be determined using the following formulas.

	Figure	Area Formula	Statement
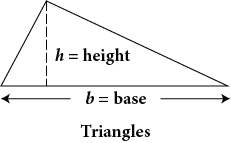
	Triangle	A = b ⋅ h	Area of a triangle is one-half the base times the height.
	Rectangle	A = l ⋅ w	Area of a rectangle is the length times the width.
	Parallelogram	A = b ⋅ h	Area of a parallelogram is base times the height.
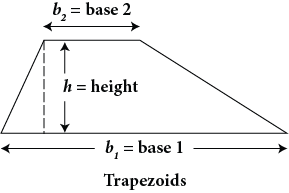
	Trapezoid	A = ⋅( b₁ + b₂ )⋅ h	Area of a trapezoid is one half the sum of the two bases times the height.
	Circle	A = πr²	Area of a circle is π times the square of the radius.
Based on the chart above, geometric figures have different formulas for area depending on their shape. Take a look at some examples.

Examples: Finding Areas of Common Geometric Figures

Find the area of the triangle.

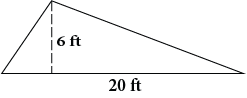
A 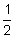triangle with height 6 feet and length 20 feet.

A = one-half ⋅ b ⋅ h = 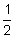⋅ 20 ⋅ 6 sq. ft. = 10 ⋅ 6 sq. ft. = 60 sq. ft. = 60 ft²

The area of this triangle is 60 sq. ft. which is often written as 60 ft².

Find the area of the rectangle.

A rectangle with width 4 feet 2 inches and height 8 inches.

Before you can calculate the area, you need the lengths of the sides to be in the same units.

1) First, convert 4 ft. 2 in. to inches.

Convert 4 inches to feet by multiplying 4 by 12; there are 12 inches in 1 foot. There are 48 inches in 4 feet. So, 4 ft. 2 in. is 48 in. + 2 in. which is 50 in.

2) Area Formula (Rectangle): A = l ∙ w

A = l ⋅ w

A = 50 in. ⋅ 8 in.

A = 400 sq. in.

Answer: The area of this rectangle is 400 sq. in.

Find the area of the parallelogram.

A parallelogram with base 10.3cm and height 6.2cm

A = b ⋅ h = 10.3 cm ⋅ 6.2 cm = 63.86 sq. cm

The area of this parallelogram is 63.86 sq. cm.

A trapezoid with height 4.1mm, bottom base 20.4mm, and top base 14.5mm.

Find the area of the trapezoid.

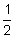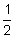A = one-half ⋅ (b₁ + b₂) ⋅ h

A = one-half ⋅ (14.5 mm + 20.4 mm) ⋅ (4.1 mm)= 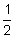⋅ (34.9 mm) ⋅ (4.1 mm) = 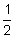⋅ (143.09 sq. mm)

A = 71.545 sq. mm

The area of this trapezoid is 71.545 sq. mm.

Find the approximate area of the circle.

A circle with radius 16.8ft.

A = π⋅r²≈ (3.14) ⋅ (16.8 ft.)² ≈ (3.14) ⋅ (282.24 sq. ft.) ≈ 888.23 sq. ft.

The area of this circle is approximately 886.23 sq. ft.

Visit the following Web site for additional information on how to find the area of common geometric figures.

Area of Geometric Figures: Plane Shapes

Now that you have reviewed the formulas and examples, it is time to watch some videos by Khan Academy. These videos will provide you with additional explanations and demonstrations of calculating area to help you gain a deeper understanding of the concepts.

Math Video Toolkit:

Area Basics

Area of Rectangles and Triangles

Area of a Circle

Exercise: Finding the Area

Now you get a chance to work out some problems. You will need to take out a sheet of paper and a pencil to complete the practice activity. You may use a calculator if you would like. Study each of these problems carefully; you will see similar problems on the lesson knowledge check.

Select the following link to complete the practice activity.

Solving for Area Practice Problems

Once you complete the practice activity, check to see how well you did by selecting the following link:

Solutions: Solving for Area Practice Problems

Summarizing Your Learning

In this lesson, you were introduced to various geometric figures and the formulas for calculating their areas. This information can be used for calculating the areas of TV screens, computer monitors, camera lenses, and so much more.

Most courses that you will take in college or technical schools may not always include specific examples that apply to your program of study. Instead, they typically give a broad overview of key concepts to leave you wanting more. As with previous lessons, you are encouraged to research how each concept relates to the field of study you have chosen. This process of inquiry is an invaluable part of your education; don't miss this opportunity to advance your knowledge.

Assessing Your Learning

Now that you have read over the lesson carefully and attempted the practice problems, it is time for a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting.

Complete the Geometric Figures: Solving for Area.

Resource:

“Measurement and Geometry: Area and Volume of Geometric Figures and Objects” by Ellis, W., & Burzynski, D. © 2010 retrieved from http://cnx.org/content/m35023/1.2/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This is an adaption of the lesson titled, “Geometric Figures and Solving for Area,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0

Additional Attributions

Have You Met The Objectives For This Lesson?