Introduction: Connecting Your Learning
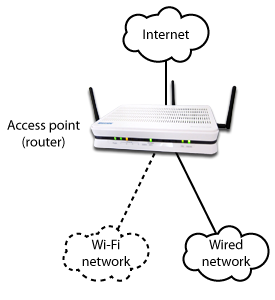 In this module you will be introduced to right triangles and how to use the Pythagorean Theorem to find the measurement of a missing side. This can be useful in finding the distances between a wireless access point (WAP) and a computer or device that is trying to access it. Some companies may install the WAP within the ceiling. WAPs always have an effective range that the receiving device must fall within. If a device is outside of that range, the computer cannot find it. If someone is having a hard time connecting to the wireless network, you might use right triangles to determine if the device is within range of the WAP.
In this module you will be introduced to right triangles and how to use the Pythagorean Theorem to find the measurement of a missing side. This can be useful in finding the distances between a wireless access point (WAP) and a computer or device that is trying to access it. Some companies may install the WAP within the ceiling. WAPs always have an effective range that the receiving device must fall within. If a device is outside of that range, the computer cannot find it. If someone is having a hard time connecting to the wireless network, you might use right triangles to determine if the device is within range of the WAP.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Identify right triangles.
- Apply the Pythagorean Theorem.
Presentation
Identifying a Right Triangle
Right Triangles
A triangle has three sides and three angles. You will need to know the definition of a right triangle to move forward in learning about the Pythagorean Theorem.
A right triangle is a triangle that has one angle whose measure is 90°.
- A right triangle CANNOT have two 90º angles. This is because the angles of a triangle must add up to 180°.
- With one angle measuring 90°, the other two angles in the right triangle must add up to 90°.
Pythagorean Theorem
In 570 BC, a mathematician named Pythagoras discovered a relationship between the sides of a right triangle. It later became known as the Pythagorean Theorem. This theorem applies to any right triangle, and is used to find the missing side of a triangle when given 2 sides.
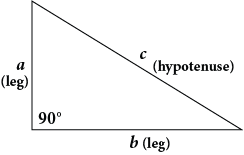
The Pythagorean Theorem states: a2 + b2 = c2
The variables a, b, and c are used to represent the sides of a right triangle.
- a and b are the "legs" of the triangle, which are the two sides that make up the 90 degree angle.
- c is the "hypotenuse" of the triangle, and is the side of the triangle that is opposite the right angle (another way to say a 90º angle is "right angle"). The hypotenuse is also the longest side of the right triangle.
Example 1
If you know that the legs of a triangle are 3 ft and 4 ft long, what is the length of the hypotenuse?
| a2 + b2 = c2 | Pythagorean Theorem One leg squared plus another leg squared is equal to the hypotenuse squared. |
 |
| 32 + 42 = c2 | The legs are 3 and 4 feet long. Therefore, a is equal to 3, and b is equal to 4. Three squared plus four squared is equal to c squared. |
|
| 9 + 16 = c2 | The sum of two sides squared is equal to c squared. | |
| 25 = c2 | Twenty five is equal to c squared. | |
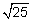 = c = c |
Take the square root of each side to find c. | |
| c = 5 | The square root of 25 is 5. | |
Example 2
If the hypotenuse of a triangle is 7 m and one of the legs of the triangle is 5 m, what is the length of the third leg of the triangle?
| a2 + b2 = c2 | Pythagorean Theorem | |
| 52+ b2= 72 | One leg is 5 m; replace a with 5. The hypotenuse is 7 m; replace c with 7. |
|
| 25+ b2 = 49 | To calculate b2, subtract 25 from 49. | |
| b2 = 24 | ||
b = 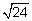 |
Take square root of each side to find b. | |
If you have reviewed the examples and would like additional information on square roots and how to find the square root of a number, go to the following Web site for an in-depth explanation, worked examples, and practice. Complete Steps 1-4.
Next watch the following Khan Academy video about the Pythagorean Theorem. You will see additional examples that can help you to better understand this new concept.
Math Video Toolkit |
Practice Exercise: Applying the Pythagorean Theorem
Now you get a chance to work out some problems. You will need a paper and a pencil to complete the following practice problems. You may use a calculator if you would like. Study each of these problems carefully; you will see similar problems on the lesson knowledge check. When you are done check your answers to see how well you did.
Practice
Using the triangle below, answer Questions 1 – 4 using the Pythagorean Theorem (triangle will not be to scale for all problems).
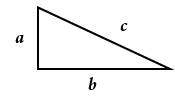
1) Assuming a = 3 ft. and c = 5 ft., calculate the measurement for side b.
2) Find the measurement for side c if a = 5 in. and b = 12 in.
3) If b = 10 cm and c = 20 cm, what does a equal?
4) If c = 25 yd. and a = 7 yd., what does b equal?
5) If a = 2 and c= 12, what does b equal?
Summarizing Your Learning
In this lesson, you have learned about right triangles and how to use the Pythagorean Theory to find the missing side. For additional information select the following link.
This brief study does not even begin to scratch the surface of what can be discovered about geometry. After researching how geometry will play a role in your particular area of study, you should be motivated to continue investigating this important subject.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice problems, it is now time to check your knowledge. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
- Complete the Geometric Figures: Right Triangles.
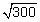 cm = 17.32 cm
cm = 17.32 cm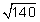 = 11.83
= 11.83