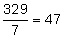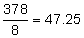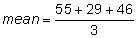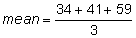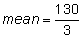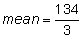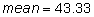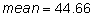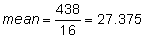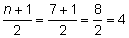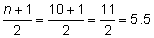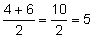Introduction: Connecting Your Learning
 In real-world applications, you can use tables and graphs of various kinds to show information and to extract information from data that can lead to analyses and predictions. Graphs allow you to communicate a message from data.
In real-world applications, you can use tables and graphs of various kinds to show information and to extract information from data that can lead to analyses and predictions. Graphs allow you to communicate a message from data.
Measures of central tendency are a key way to discuss and communicate with graphs. The term central tendency refers to the middle, or typical, value of a set of data, which is most commonly measured by using the three m's: mean, median, and mode. The mean, median, and mode are known as the measures of central tendency. In this lesson, you will explore these three concepts.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Compute the mean, median, and mode of a given set of data.
- Identify an outlier given a set of data.
- Identify the mode or modes of a data set for both quantitative and qualitative data.
Key Terms
Presentation
The Mean, Median, and Mode
Mean, median, and mode are three basic ways to look at the value of a set of numbers. You will start by learning about the mean.
The mean, often called the average, of a numerical set of data, is simply the sum of the data values divided by the number of values. This is also referred to as the arithmetic mean. The mean is the balance point of a distribution.
| Mean = | sum of the values |
| the number of values |
For instance, take a look at the following example. Use the formula to calculate the mean number of hours that Stephen worked each month based on the example below.
| Example | |
Problem |
Stephen has been working on programing and updating a Web site for his company for the past 15 months. The following numbers represent the number of hours Stephen has worked on this Web site for each of the past 7 months: 24, 25, 31, 50, 53, 66, 78 What is the mean (average) number of hours that Stephen worked on this Web site each month? |
Step 1: Add the numbers to determine the total number of hours he worked. 24 + 25 + 33 + 50 + 53 + 66 + 78 = 329 |
|
Step 2: Divide the total by the number of months. |
|
The calculations for the mean of a sample and the total population are done in the same way. However, the mean of a population is constant, while the mean of a sample varies from sample to sample.
| Example | |
Problem |
Mark operates Technology Titans, a Web site service that employs 8 people. Find the mean age of his workers if the ages of the employees are as follows: 55, 63, 34, 59, 29, 46, 51, 41 |
Step 1: Add the numbers to determine the total age of the workers.
Step 2: Divide the total by the number of months. |
|
Look at another approach. If you were to take a sample of 3 employees from the group of 8 and calculate the mean age for these 3 workers, would the results change?
Use the ages 55, 29, and 46 for one sample of 3, and the ages 34, 41, and 59 for another sample of 3:
The mean age of the first group of 3 employees is 43.33 years.
The mean age of the second group of 3 employees is 44.66 years.
The mean age for a sample of a population depends upon the values that are included in the sample. From this example, you can see that the mean of a population and that of a sample from the population are not necessarily the same.
In addition to calculating the mean for a given set of data values, you can apply your understanding of the mean to determine other information that may be asked for in everyday problems.
| Example | |
Problem |
Two weeks before Mark opened Technology Titans, he launched his company Web site. During those 14 days, Mark had an average of 24.5 hits on his Web site per day. In the first two days that Technology Titans was open for business, the Web site received 42 and 53 hits respectively. Determine the new average for hits on the Web site. |
Step 1: Multiply the given average by 14 to determine the total number of hits on Mark's Web site.
Step 2: Add the hits for the first two days his business was open.
Step 3: Divide this new total by 16 to determine the new average. |
|
All values for the means you have calculated so far have been for ungrouped, or listed, data. A mean can also be determined for data that is grouped, or placed in intervals. Unlike listed data, the individual values for grouped data are not available, and you are not able to calculate their sum. To calculate the mean of grouped data, the first step is to determine the midpoint of each interval or class. These midpoints must then be multiplied by the frequencies of the corresponding classes. The sum of the products divided by the total number of values will be the value of the mean.
The following example will show how the mean value for grouped data can be calculated.
| Example | |||
Problem |
In Tim's office, there are 25 employees. Each employee travels to work every morning in his or her own car. The distribution of the driving times (in minutes) from home to work for the employees is shown in the table below. |
||
|
|||
Calculate the mean of the driving times. |
|||
Step 1: Determine the midpoint for each interval. For 0 to less than 10, the midpoint is 5. For 10 to less than 20, the midpoint is 15. For 20 to less than 30, the midpoint is 25. For 30 to less than 40, the midpoint is 35. For 40 to less than 50, the midpoint is 45. Step 2: Multiply each midpoint by the frequency for the class. For 0 to less than 10, (5)(3) = 15 For 10 to less than 20, (15)(10) = 150 For 20 to less than 30, (25)(6) = 150 For 30 to less than 40, (35)(4) = 140 For 40 to less than 50, (45)(2) = 90 Step 3: Add the results from Step 2 and divide the sum by 25. 15 + 150 + 150 + 140 + 90 = 545 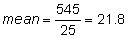
|
|||
The mean is often used as a summary statistic. However, it is affected by extreme values (outliers): either an unusually high or low number. When you have extreme values at one end of a data set, the mean is not a very good summary statistic.
Example: Outliers
If you were employed by a company that paid all of its employees a salary between $60,000 and $70,000, you could probably estimate the mean salary to be about $65,000.
However, if you had to add in the $150,000 salary of the CEO when calculating the mean, then the value of the mean would increase greatly. It would, in fact, be the mean of the employees' salaries, but it probably would not be a good measure of the central tendency of the salaries.
In addition to calculating the mean for a given set of data values, you can also apply your understanding of the mean to determine other information that may be asked for in everyday problems.
The Median
What is the Median?
The median is the number that falls in the middle position once the data has been organized. Organized data means the numbers are arranged from smallest to largest or from largest to smallest. The median for an odd number of data values is the value that divides the data into two halves. If n represents the number of data values and n is an odd number, then the median will be found in the 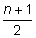 position.
position.
This measure of central tendency is typically used when the mean value is affected by an unusually low number or an unusually high number in the data set (outliers). Outliers distort the mean value to the extent that the mean value no longer accurately depicts the set of data.
For example: If one of the houses in your neighborhood was broken down and maintained a low property value, then you would not want to include this property when determining the value of your own home. However, if you are purchasing a home in that neighborhood, you may want to include the outlier since it would drive down the price you would have to pay.
Try a few examples to follow the steps needed to calculate the median.
| Example | |
Problem |
Find the median of the following data:
|
Step 1: Organize the data, or arrange the numbers from smallest to largest.
Step 2: Since the number of data values is odd, the median will be found in the Step 3: In this case, the median is the value that is found in the fourth position of the organized data.
|
|
Another way to look at the example is to narrow the data down to find the middle number.
2, 6, 8, 10, 12, 14, 16
Χ, 6, 8, 10, 12, 14, Χ
Χ, Χ, 8, 10, 12, Χ, Χ
Χ, Χ, Χ, 10, Χ, Χ, Χ
Here is another example of how to calculate the median of a set of numbers.
| Example | |
Problem |
Find the median of the following data:
|
Step 1: Organize the data, or arrange the numbers from smallest to largest.
Step 2: Since the number of data values is even, the median will be the mean value of the numbers found before and after the Step 3: The number found before the 5.5 position is 4 and the number found after the 5.5 position is 6. Now, you need to find the mean value.
|
|
The Mode
What is the Mode?
The mode of a set of data is simply the value that appears most frequently in the set.
If two or more values appear with the same frequency, each is a mode. The downside to using the mode as a measure of central tendency is that a set of data may have no mode, or it may have more than one mode. However, the same set of data will have only one mean and only one median.
- The word modal is often used when referring to the mode of a data set.
- If a data set has only one value that occurs most often, the set is called unimodal.
- A data set that has two values that occur with the same greatest frequency is referred to as bimodal.
- When a set of data has more than two values that occur with the same greatest frequency, the set is called multimodal.
When determining the mode of a data set, calculations are not required, but keen observation is a must. The mode is a measure of central tendency that is simple to locate, but it is not used much in practical applications.
| Example | |
Problem |
Find the mode of the following data: 76, 81, 79, 80, 78, 83, 77, 79, 82, 75 |
There is no need to organize the data, unless you think that it would be easier to locate the mode if the numbers were arranged from least to greatest. In the above data set, the number 79 appears twice, but all the other numbers appear only once. Since 79 appears with the greatest frequency, it is the mode of the data values. |
|
| Example | |
Problem |
The ages of 12 randomly selected customers at a local Best Buy are listed below: 23, 21, 29, 24, 31, 21, 27, 23, 24, 32, 33, 19 What is the mode of the above ages? |
The above data set has three values that each occur with a frequency of 2. These values are 21, 23, and 24. All other values occur only once. Therefore, this set of data has three modes. |
|
Remember that the mode can be determined for qualitative data as well as quantitative data, but the mean and the median can only be determined for quantitative data.
| Example | |
Problem |
You begin to observe to the color of clothing your employees wear. Your goal is to find out what color is worn most frequently so that you can offer company shirts to your employees. Monday: Red, Blue, Black, Pink, Green, and Blue Tuesday: Green, Blue, Pink, White, Blue, and Blue Wednesday: Orange, White, White, Blue, Blue, and Red Thursday: Brown, Black, Brown, Blue, White, and Blue Friday: Blue, Black, Blue, Red, Red, and Pink What is the mode of the colors above? |
The color blue was worn 11 times during the week. All other colors were worn with much less frequency in comparison to the color blue. |
|
Now that you have added to your knowledge by reviewing the lesson and the examples, it is time to watch the following Khan Academy videos. These videos will provide additional explanations and working examples of how to determine the mean, median, and mode to help you gain a better understanding of this new concept.
 |
Math Video Toolkit |
Practice Exercise: Mean, Median, and Mode
 |
Now you get a chance to work out some problems. You may use a calculator if you would like. Study each of these problems carefully; you will see similar problems on the lesson knowledge check. Select the following link to complete the practice activity. You will need to get out a piece of paper and a pencil to complete the practice problems. Mean, Median, and Mode Practice Problems Once you complete the practice activity, check to see how well you did by selecting the following link: |
Summarizing Your Learning
In this lesson, you have learned how to calculate the mean, median, and mode of a set of data values. In addition, you have been introduced to other key terms such as measures of central tendency, unimodal, bimodal, and outliers. You also learned that the mode is the only measure of central tendency used in both quantitative and qualitative data.
As with every lesson and module, you are encouraged to research how these topics pertain to your particular area of study within the world of information technology. By now you are very aware that not every topic in mathematics will be directly implemented in your future career field. However, do not rule out the possibility that this topic might be an integral part of your future until you do some research.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice problems, it is time for a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
1) Complete the Statistics: Finding Mean, Median, and Mode.
Resource:
“Chapter 5: Measures of Central Tendency” by Merry, B. © 2012 retrieved from http://www.ck12.org/flexbook/chapter/9079 and used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This is an adaption of the lesson titled, “Measures of Central Tendency: Mean, Median, and Mode” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0