Introduction: Connecting Your Learning
 Many students ponder whether they will ever use math after graduation. It can be hard to imagine yourself using trigonometry or calculus. However, when entering the world of information technology (IT), you will be exposed to a gamut of topics related to mathematics, possibly even using formulas that expand far beyond your range of understanding or comfort. In this lesson, you will be introduced to two financial planning formulas (simple interest and compound interest). Don't view the topic as a study of finance but more as a study of how to work with formulas even when you are uncertain about how they were created or how they produce an answer to the question. In the IT world, you will find many jobs that require you to be formula savvy.
Many students ponder whether they will ever use math after graduation. It can be hard to imagine yourself using trigonometry or calculus. However, when entering the world of information technology (IT), you will be exposed to a gamut of topics related to mathematics, possibly even using formulas that expand far beyond your range of understanding or comfort. In this lesson, you will be introduced to two financial planning formulas (simple interest and compound interest). Don't view the topic as a study of finance but more as a study of how to work with formulas even when you are uncertain about how they were created or how they produce an answer to the question. In the IT world, you will find many jobs that require you to be formula savvy.
For example, suppose you are developing a mobile finance application. One of the features you want to include to make your app stand out above the rest is an interest calculator that integrates into the customer's checkbook. In this scenario, understanding how the simple interest formula and compound interest formula calculate interest will help you program the feature correctly.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Solve financial problems that involve simple interest.
Presentation
Simple Interest
It costs money to borrow money, and the "rent" one pays for using money is called the interest. The amount of money being borrowed or loaned is called the principal or present value. Simple interest is paid only on the original amount borrowed. When the money is loaned out, the person who borrows the money generally pays a fixed rate of interest on the principal for the time period he or she keeps the money. Although the interest rate is often specified for a year, it may be specified for a week, a month, or a quarter, etc. Credit card companies often list their charges as monthly rates, sometimes as high as 1.5% a month.
If an amount P is borrowed for a time t at an interest rate of r per time period, then the simple interest is given by
I = P ⋅ r ⋅ t
The simple interest formula is I = P ⋅ r ⋅ t
In this formula P represents the amount borrowed or the original amount.
- r represents the interest rate.
- t is the time – in years.
A couple of things to remember:
The interest rate will be given to you as a percentage.
- To make the formula work correctly, you'll first need to change the percentage to a decimal.
- You can change a percentage to a decimal by moving the decimal point two places to the left. The chart below shows some examples:
Given Percentage |
Decimal Equivalent |
234.9% |
2.349 |
65.3% |
0.653 |
7% |
0.07 |
0.004% |
0.00004 |
As stated, t in the formula represents time, in years. If your loan was for 6 months, you would have to translate that into years. You know that 6 months is one-half of a year, so t = 0.5. Suppose the length of the loan is 33 months. To change 33 months into years you would need to divide 33 by 12 because there are 12 months in a year. So 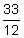 = 2.75. 33 months is 2.75 years.
= 2.75. 33 months is 2.75 years.
But what if the loan was for an odd length of time like 7 months? The term of 7 months changes to 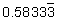 years. What can you do then? Depending on how accurate your answer needs to be, you could round the number to an appropriate place: perhaps 0.58333, 0.583, or even 0.6. You could also work with the term as a fraction:
years. What can you do then? Depending on how accurate your answer needs to be, you could round the number to an appropriate place: perhaps 0.58333, 0.583, or even 0.6. You could also work with the term as a fraction: 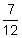 .
.
Example 1
Since Ursula needs money to buy computer software, she borrows $600 for 9 months at a simple interest rate of 15% per year. Find the amount of interest Ursula will be responsible for paying.
Solution
Use the formula I = P r t.
You need to find I. The amount borrowed, $600, is P. The interest rate is 15%.
Because you need a decimal, you change the 15% to 0.15.
The time is 9 months, so 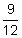 is 0.75 years.
is 0.75 years.
The formula becomes I = 600 ⋅ 0.15 ⋅ 0.75
Multiplying this out, the calculator gives you 67.5. Therefore, the amount of interest Ursula will be paying on this loan is $67.50.
The total amount due, A, also called the accumulated value or the future value, is given by
A = P + I
Amount = Principal + Interest
The total amount you have to pay back (A) is equal to the amount borrowed (P) plus the Interest due (I).
Back to Example 1, Ursula borrowed $600 and owes $67.50 in interest. So the accumulated value would be 600 + 67.50, or $667.50.
Example 2
Jerry is going to ask his father for a loan to buy a $1,200 mountain bike. His dad agrees to loan Jerry the $1,200 as long as Jerry agrees to pay 8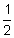 % interest for the 18 months he has the loan. Jerry agreed to his father's terms and bought his bike. At the end of the 18 months, how much will Jerry have to give his father?
% interest for the 18 months he has the loan. Jerry agreed to his father's terms and bought his bike. At the end of the 18 months, how much will Jerry have to give his father?
Solution:
- First you need to find out how much interest Jerry will owe at the end of the loan period. You know that 8
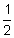 %, written as a decimal, is 8.5% which changes to 0.085 as a decimal.
%, written as a decimal, is 8.5% which changes to 0.085 as a decimal. - The loan term is 18 months or 1.5 years (
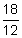 ).
). - Remember I = Prt, which means I = 1,200 ⋅ 0.085 ⋅ 1.5.
- Jerry owes his dad $153 in interest.
- Next you must figure out the total amount Jerry will be paying his dad.
A = P + I, so A = 1,200 + 153 = 1,353.
Jerry will give his father $1,353 at the end of the 18 months.
- Working with the original formula, A = P + I, you can replace the I with Prt. Remember that I = Prt. So, A = P + Prt.
- Now, remember the distributive property from Lesson 2: a (b + c) = ab + ac.
- You've got P + Prt. Using the distributive property, you get P (1 + rt). It might be a little difficult to see right away, but think of it as the distributive property backwards.
- Remember also that P ⋅ 1 = P. If you multiply out the P (1 + rt) you get P + Prt.
So A = P + I → A = P + Prt → A = P (1 + rt)
Knowing this, you can revisit Example 2 and simplify the calculation:
A = P (1 + rt) becomes A = 1,200(1 + 0.085 ⋅ 1.5)
- It is important to remember the order of operations.
- The calculations inside the parentheses come first.
- Multiplication comes before addition, so you multiply 0.085 times 1.5 first, and then add the 1.
- A = 1,200(1 + 0.1275) = 1,200(1.1275) = 1,353.
- By calculating the problem a different way, you see that Jerry owes his father the same amount: $1,353.
Example 3
José received a bonus check for $2,500. He deposited it in an account that pays 2% simple interest. How much money will he have at the end of 3 years?
Solution:
The total amount or the future value is given by A=P (1+rt).
A = $2,500[1+ (0.02)(3)]= $2,500(1.06) = $2,650
Example 4
Here is a slightly different problem: Darnel owes a total of $3,330 for purchasing a brand-new computer with all the extras. It includes 12% interest for the 4 years he borrowed the money. How much did he originally borrow?
Solution:
This time you are asked to compute the principal, P.
Use A=P(1+rt). A is $3,330, r is 0.12, and t is 4.
$3,330 = P[1 + (0.12)(4)]
3330 = P(1.48)
To solve for P, you'll need to divide by 1.48.
 = 2250
= 2250
So Darnel originally borrowed $2,250.
Example 5
You have a loan that you need to pay back now that the two-and-one-half-year period has passed. Your calculation shows that you need to pay back $2,281.23. If the loan had an interest rate of 9.7%, how much did you originally borrow?
Solution:
A = P(1 + rt)
2281.23 = P(1 + 0.097 2.5)
2281.23 = P(1.2425)
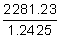 = 1836
= 1836
You originally borrowed $1,836.
Compound Interest
In the previous section, the problems involved simple interest. Simple interest is charged when the lending period is short, often less than a year. When the money is loaned or borrowed for a longer time period and the interest is paid (or charged) not only on the principal, but also on the past interest, the interest is compounded.
Suppose you deposit $200 in an account that pays 2.75% interest.
- At the end of one year, you will have $200 + $200(.0275) = $200 (1+.0275) = $205.50.
Now suppose you put this amount, $205.50, in the same account.
- After another year, you will have $205.50 + $205.50 (.015) = $205.50 (1+.015) =$211.15.
So an initial deposit of $200 has accumulated to $211.15 in two years. (Note)
The reason the amount is slightly higher than you would earn with a simple interest account is that the interest ($5.50) earned the first year was put back into the account. This $5.50 amount earned interest $5.50(.0275) = $.15 in one year, thus resulting in the increase. You have earned interest on the principal as well as on the past interest, and that is why it is called compound interest.
Now suppose you leave this amount, $211.15, in the bank for another year; the amount in the account after the third year will be $211.15 + $211.15(.0275) = $211.15(1+.0275) = $216.96.
Examine the mathematical part of this problem to devise an easier way to solve these problems.
After one year, you had
$200(1+.0275) = $205.50 (first step)
After two years, you had
$205.50(1+.0275) = 211.15 (second step)
Noticing $205.50=$200(1+.0275), from the first step, the second step becomes
$200(1+.0275)(1+.00275)=$211.15
After three years, you get
$200(1+.00275) (1+.00275)(1+.0275) which is $216.96.
$216.96 can also be written as:
$200(1+.0275)3 =$216.96
Suppose you are asked to find the total amount at the end of 5 years, you will get:
$200(1+.0275)5 =$229.05
You can summarize the calculations as follows: |
||
| The original amount | $200 | =$200 |
| The amount after one year | $200(1+.0275) | =$205.50 |
| The amount after two years | $200(1+.0275)2 | =$211.15 |
| The amount after three years | $200(1+.0275)3 | =$216.96 |
| The amount after five years | $200(1+.0275)5 | =$229.05 |
| The amount after t years | $200(1+.0275)t | |
Banks often compound interest more than one time per year. Consider a bank that pays 2% interest but compounds it quarterly or four times a year. This means that every quarter, the bank will pay interest equal to one-fourth of 2%, or .5%. Take a look at the following example and make sure you click the note to the right of the problem for additional information.
To show how this works assume that you have deposited $500 in the bank. The following is a breakdown of how the compound interest would be calculated.
| The original amount | $500 | = $500 |
| The amount after one quarter | $500(1+ 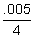 ) ) |
= $500.63 |
| The amount after two quarters | $500(1+ 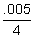 )2 )2 |
= $501.25 |
| The amount after one year | $500(1+ 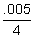 )4 )4 |
= $502.50 (Note) |
| The amount after two years | $500(1+ 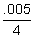 )8 )8 |
= $505.02 (Note) |
| The amount after three years | $500(1+ 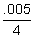 )12 )12 |
= $507.55 |
| The amount after five years | $500(1+ 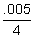 )20 )20 |
= $512.65 |
| The amount after t years | $500(1+ 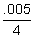 )4t )4t |
Therefore, if you invest a lump-sum amount of P dollars, at an interest rate of r, compounded n times a year, after t years you will have:
A=P(1 + 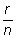 )nt
)nt
Now that you have gained an understanding of how to solve problems with interest, watch the following videos to learn more about interest rates. You will get to see additional examples that can help you gain a better understanding of this new concept.
 |
Math Video Toolkit: Sophia Learning: Interest Tutorial Khan Academy: Introduction to Interest Part 1 Khan Academy: Introduction to Interest Part 2 |
Practice Exercises: Interest Rates
You will need a piece of paper and a pencil to complete the following practice problems. You may use a calculator. Once you complete the practice problems, check your answers to see how well you did.
Practice Problem 1
If $3,500 is invested at 2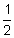 % compounded monthly, what will the future value be in 4 years?
% compounded monthly, what will the future value be in 4 years?
Practice Problem 2
You sold your idea for a software game to a gaming company for $1,500. You invest that money in a savings account paying 3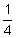 % compounded semi-annually. If you don't touch the money for 10 years, how much will the account be worth then?
% compounded semi-annually. If you don't touch the money for 10 years, how much will the account be worth then?
Now select the following links to complete additional practice problems.
Compound Interest Practice Quiz
Summarizing Your Learning
In this lesson, you have worked with two significant finance formulas. The key to correctly calculating the solution starts with knowing what each variable represents. Often when faced with problems in everyday life, you are not given facts and figures in an organized word problem like the ones seen in this lesson. Your job is to decipher the facts and amounts into meaningful information that fits within the formula. Once this is accomplished, calculating the result using the order of operations becomes the easy part.
Now that you have completed this lesson, take the opportunity to conduct additional research into how these topics pertain to your particular area of study within the IT world. At times students may miss the most obvious purpose behind the study of mathematics, the ability to think logically and to creatively solve problems. Many jobs and hobbies will require a quick mind and the ability to think on your feet. Mathematics and other topics give your mind the training needed to obtain these skills.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice problems, it is time for a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
- Complete the Arithmetic Review: Interest Rates Numbers.
Resource:
“Mathematics of Finance” by Sekhon, R. © 2011 retrieved from http://cnx.org/content/m18905/1.2/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This is an adaption of the lesson titled, “Interest Rates,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0.
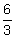 is 2
So when we’re looking for a process, let’s use what we know to point us in the right direction.
6 = P ⋅ 3, we know the answer is 2, and to get 2, we take 6 and divide it by 3.
is 2
So when we’re looking for a process, let’s use what we know to point us in the right direction.
6 = P ⋅ 3, we know the answer is 2, and to get 2, we take 6 and divide it by 3. 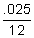 every month for four years, or 48 times. To translate this to our formula we find:
every month for four years, or 48 times. To translate this to our formula we find: 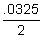 )2*10
)2*10