Introduction: Connecting Your Learning
 In a previous lesson, you were introduced to various applications for the United States Measurement System. Many computer standards are developed by an international governing body. Therefore, when standards are developed for wireless and network technologies, mobile device development, geospatial technologies, and others, the Metric System of Measurement is usually used, so it is essential to become familiar with both measurement systems.
In a previous lesson, you were introduced to various applications for the United States Measurement System. Many computer standards are developed by an international governing body. Therefore, when standards are developed for wireless and network technologies, mobile device development, geospatial technologies, and others, the Metric System of Measurement is usually used, so it is essential to become familiar with both measurement systems.
This module discusses the Metric System of Measurement, advantages of the base ten number system, prefixes, and conversion from one unit of measure in the metric system to another.
Focusing Your Learning
Lesson Objectives
By the end of this lesson, you should be able to:
- Convert units of measurement using the Metric System.
Presentation
The Advantages of the Base Ten Number System
The metric system of measurement takes advantage of the base ten number system. The advantage to using metric system over the United States system is that in the metric system, it is possible to convert from one unit of measure to another by multiplying or dividing the given number by a power of 10. This means you can make a conversion simply by moving the decimal point to the right or the left.
Prefixes
Common units of measure in the metric system are the meter (for length), the liter (for volume), and the gram (for mass). A prefix can be attached to each unit. The metric prefixes along with their meaning are listed below.
Metric Prefixes
kilo — thousand
hecto — hundred
deka — ten
deci —tenth
centi — hundredth
milli — thousandth
For example, if length is being measured the following are true:
1 kilometer is equivalent to 1,000 meters.
1 centimeter is equivalent to one hundredth of a meter.
1 millimeter is equivalent to one thousandth of a meter.
Conversion from One Unit to Another Unit
Three characteristics of the metric system occur in the metric table of measurements.
- In each category, the prefixes are the same.
- You can move from a larger to a smaller unit of measure by moving the decimal point to the right.
- You can move from a smaller to a larger unit of measure by moving the decimal point to the left.
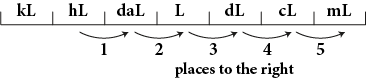
The following table provides a summary of the relationship between the basic unit of measure (meter, gram, liter) and each prefix, and how many places the decimal point is moved and in what direction.
kilo hecto deka unit deci centi milli
| Basic Unit to Prefix | Move the Decimal Point | |
| unit to deka | 1 to 10 | 1 place to the left |
| unit to hecto | 1 to 100 | 2 places to the left |
| unit to kilo | 1 to 1,000 | 3 places to the left |
| unit to deci | 1 to 0.1 | 1 place to the right |
| unit to centi | 1 to 0.01 | 2 places to the right |
| unit to milli | 1 to 0.001 | 3 places to the right |
Conversion Table
Listed below, in the unit conversion table, are some of the common metric units of measure.
| Unit Conversion Table | ||
| Length | 1 kilometer(km)=1,000 meters(m) | 1,000×1 m |
| 1 hectometer(hm)=100 meters | 100×1 m | |
| 1 dekameter(dam)=10 meters | 10×1 m | |
| 1 meter (m) | 1×1 m | |
1 decimeter(dm)= 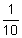 meter meter |
.1×1 m | |
1 centimeter(cm)= 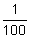 meter meter |
.01×1 m | |
1 millimeter(mm)= 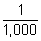 meter meter |
.001×1 m | |
| Mass | 1 kilogram(kg)=1,000 grams(g) | 1,000×1 g |
| 1 hectogram(hg)=100 grams | 100×1 g | |
| 1 dekagram(dag)=10 grams | 10×1 g | |
| 1 gram (g) | 1×1 g | |
1 decigram(dg)= 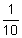 gram gram |
.1×1 g | |
1 centigram(cg)= 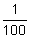 gram gram |
.01×1 g | |
1 milligram(mg)= 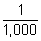 gram gram |
.001×1 g | |
| Volume | 1 kiloliter(kL)=1,000 liters(L) | 1,000×1 L |
| 1 hectoliter(hL)=100 liters | 100×1 L | |
| 1 dekaliter(daL)=10 liters | 10×1 L | |
| 1 liter (L) | 1×1 L | |
1 deciliter(dL)= 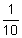 liter liter |
.1×1 L | |
1 centiliter(cL)= 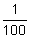 liter liter |
.01×1 L | |
1 milliliter(mL)= 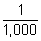 liter liter |
.001×1 L | |
| Time | Same as the United States System | |
Distinction Between Mass and Weight
There is a distinction between mass and weight. The weight of a body is related to gravity whereas the mass of a body is not. For example, your weight on the earth is different than it is on the moon, but your mass is the same in both places. Mass is a measure of a body's resistance to motion. The more massive a body, the more resistant it is to motion. Also, more massive bodies weigh more than bodies with less mass.
Converting Metric Units
To convert from one metric unit to another metric unit:
- Determine the location of the original number on the metric scale (pictured in each of the following examples).
Move the decimal point of the original number in the same direction and the appropriate number of places to move to the desired metric unit.
You can also convert from one metric unit to another using unit fractions. Take a look at some examples.
Example 1
The weight of a computer screen is 3 kg. Convert the measurement to g.
(a) 3 kg can be written as 3.0 kg. Then,
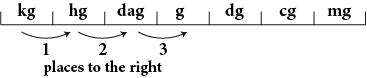
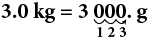
Thus, 3 kg = 3,000 g.
(b) You can also use unit fractions to make this conversion.
Since you are converting to grams, and 1,000g = 1 kg, you choose the unit fraction 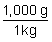 since grams is in the numerator.
since grams is in the numerator.
| 3 kg | = 3 kg ⋅ 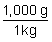 |
| = 3 ⋅ 1,000 g | |
| = 3,000 g |
Example 2
Convert 67.2 hectoliters to milliliters.
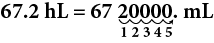
Thus, 67.2 hL = 6,720,000 mL.
Example 3
The secretary has placed her computer and a fax machine on a table which measures to 100.07 cm. Convert the measurement to meters.

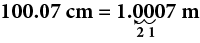
Thus, 100.07 cm=1.0007 m.
Example 4
Convert 0.16 milligrams to grams.

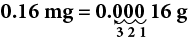
Thus, 0.16 mg=0.00016 g.
The following section provides some brief information on binary prefixes and the binary number system to help you become familiar with these terms and their meanings. The binary number system is important to the world of information technology.
Binary Numbers
A binary prefix is used to identify a unit of digital information. In order to understand binary prefixes, you must understand what binary numbers represent. Binary numbers represent numeric values using two symbols: 0 and 1. Almost all digital computers these days are binary, meaning that they deal with numbers expressed in binary rather than decimal. This means that memory addresses, and thus memory sizes, are also expressed in binary.
Select the following link to review a chart of information detailing prefixes for multiples of bits and bytes.
Prefixes for Multiples of Bits or Bytes
 |
For additional information about binary numbers select the following links. |
 |
Now that you have added to your knowledge by reviewing the lesson and the examples, it is time to watch the following Khan Academy videos. These videos will provide additional explanations and working examples of how to convert measurements within the metric system.
 |
Math Video Toolkit: |
Practice Exercise: Converting Measurements
 |
Now you get a chance to work out some problems. You may use a calculator if you would like. Study each of these problems carefully; you will see similar problems on the lesson knowledge check. Select the following link to complete the practice activity. You will need to get out a piece of paper and a pencil to complete the practice problems. Conversions using the Metric System Practice Problems Once you complete the practice activity, check to see how well you did by selecting the following link: |
Summarizing Your Learning
As you finish this module, you have seen many units of measure, and you have become familiar with the method used to convert measurements. Converting does not stop with just knowing the U.S. system and the metric system. Computers use another significant system of measurement: the conversion between bytes, megabits, kilobytes, gigabytes, terabytes, and so on. As you work with computers, this conversion automatically happens, but sometimes it is easy to forget that a computer programmer had to put this conversion aspect in place for computers to be more user-friendly. You may want to research how the binary system that is used by computers works.
Assessing Your Learning
 |
Now that you have read over the lesson carefully and attempted the practice problems it is now time to complete a knowledge check. Please note that this is a graded part of this lesson so be sure you have prepared yourself before starting. |
- Complete the Measurement: Conversions using Metric System.
Resources:
“Measurement and Geometry: Area and Volume of Geometric Figures and Objects” by Ellis, W., & Burzynski, D. © 2010 used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. This is an adaption of the lesson titled, “Metric Measurement” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0
“Prefixes” for Binary Multiples by Simpson, R. © 2005 used under a Creative Commons Attribution 2.0 http://creativecommons.org/licenses/by/2.0/. This is an adaption of the lesson titled, “Metric Measurement” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0